How Does the Matchmaker Match Players?
-
In order to understand FAF Matchmaking you're going to first be better off having a basic understanding of how TrueSkill itself works and then the problems with the system that FAF attempts to address. So let's begin with that.
TrueSkill:
Regardless of whether you're playing a teamgame or a 1v1, TrueSkill operates quite similarly for both types of games. In 1v1, the matching process is primarily centered around a player's mean (or mu) value which is the level the system is 50% confident you can play at. It then proceeds to try to find a player that is close to this mu value for you to then play a game against.Once this game is over, the system is then able to calculate the impact of this game loss upon you by reviewing player deviation (or sigma). A high sigma player is going to get a larger magnitude in change from the game result than a low sigma player. This will continue until the system is able to properly place the player after putting them against a broad range of players. This is why lower rating players are often put against people quite a bit better than them, as the matchmaker itself needs to ensure that the player is not able to beat such players and then refine the matchmaking process further.
In teamgames, individual player mu values are combined to find the team's sum mu value at which point the game is treated like a "1v1" except the 1v1 values are formed from a sum of individual values. Player individual sigma will determine the impact of the game result on the individual player.
Problem 1: New Player Mu and Sigma
In FAF, a new player is given the values of 1500 for mu and 500 for sigma. The values themselves hold no intrinsic meaning and the reasoning for why they were chosen as the set values are irrelevant. Essentially 1500 mu and 500 sigma means that the intended bell curve of FAF is meant to peak at 1500 mu and the 500 sigma means that a new player shows as "0 rated" on leaderboards, lobbies, etc.However, in FAF, the distribution of players is not the expected distribution that our TrueSkill values are meant to operate under. Namely, 1500 mu is not the top of our player distribution bell curve. There are many reasons for this but none are necessary to go into. 1500 mu is quite far off the top of our player population distribution curve and so it makes the new player experience quite awful as they are playing individuals they have nearly 0 chance of defeating in their first initial game. This makes the experience terrible for both players and also leads to inefficient data gathering for the algorithm.
So how does FAF solve it? We utilize a linear interpolation method for new players as the traditional TrueSkill method of player matching is not as practically efficient as it should theoretically be. For their first 10 games, a player will get MATCHED based on this adjusted rating when they are a new variable in the environment.
Here is a basic equation to explain how it works:
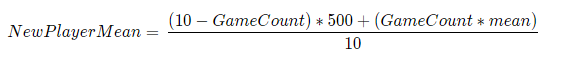
Example: A new player's mu would be:
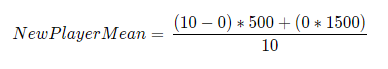
Which simplifies to 500 mu.
Note: This interpolation has no impact on how your rating is recorded within our database nor how it shows up in game. This adjustment strictly happens when the system is creating matches.
So new players should expect to match up against people at around 500 mu, which is approximately 200-300 shown rating.
Problem 2: What About Players that Play in Other Environments?
FAF has several TrueSkill elements. We have 1v1 rating, 2v2 rating, and global rating. So how does the system try to account for the fact some people have way more experience than others?Well, TrueSkill itself attempts to do through the high sigma value attached to new players. However, as we can be confident that the data attached to these other ratings have some sort of inherent value in determining the skill of an individual player, we can use this data to make the experience of transitioning between various closed environments of FAF more fluid.
What we do is we take the global mu and sigma of a player, add 150 sigma up to a maximum of 250 sigma, and then utilize this as your matchmaker rating. This will be the matchmaking rating that is recorded in the database for you and it will be what the system utilizes to determine your competency as a player PRIOR to the linear interpolation method. If this confuses you, please look at the example in the following post.
Why do we increase sigma? Because while we can be certain that a 1500 mu player in global games has a general understanding of the game that should be larger than what you would expect from an 800 mu player elsewhere in the environments on FAF, we can't be certain that it is equivalent to a 1300 mu player in these other environments. Hence, the sigma increase to account for the fact we have data of some value, but not absolutely certain data on the skill of a player as they transfer between environments.
Problem 3: Getting New Players in Games as Fast as Possible
No one likes waiting, particularly new players. It's up to us to prove that the game is fun and so we want them getting into a game as quickly as possible. For that reason, we decided to implement a controlled random matchmaking process that attempts to match new players as quickly as possible.However this has a problem that circles back to Problem 1, namely that we do not want new players matching with extremely competent players as no one will enjoy such games. So instead, we devised a way to separate a "newbie" from a "top player" and utilized that in this controlled random process.
So first some definitions:
- A top-level player is anyone with mu over 1600
- A newbie is anyone with less than 10 games.
All teams with at least one newbie and no top-rated player will be matched randomly amongst each other if no decent game is initially found. If there are an odd number of newbie teams, the last newbie team can only match with a non-newbie team that has at least one failed matching attempt. If a team has a top-rated player, that team will not be eligible for random matching at all.
-
So in order to clarify this system a bit more, I'm going to walk through an example.
Let's say we have a player that played pure astro in global games and is now 1500 rated with 150 sigma. This player would now like to play this new 2v2 matchmaker he heard about. What will happen to him?
Initially, the system will rate him by taking his global rating values (1500,150) and adding additional sigma to him to account for the potential growing pains of the player. Evidently astro gameplay is quite different from traditional 2v2 gameplay, and so a slight decrease in certainty should be expected.
This player will now be considered (1500,250) by the system. Why not 300 sigma? Because it chooses the smallest value between (global sigma+150, 250).
In addition, this player, for his first 10 games, will utilize the linear interpolation method when deciding who he will MATCH against not what his actual rating IS.
We know from the equation above that this would put him at ((10-0)x500+(0x1500))/10 or 500 mu for his first game. On his second game, he will have (9*500+1x1502)/10 or 600 mu.
You can see the player gained from 1500 mu to 1502 mu. Why such a small change? Because he faced someone around 500 mu and the system would expect an individual with 1500 mu to easily trounce someone with 500 mu. The slight adjustment reflects that. The linear interpolation will continue until the player reaches 10 games.
In addition, if this player is queueing with another player that is also below 1600 mu, then these players should be matching up quite frequently due to the random matchmaking protocol.